A neural network has been developed that simulates the behavior of a wide range of dynamical systems, including models of the Hodgkin-Huxley type, as well as ensembles based on them

About ongoing research

Within the framework of the project of the Russian Science Foundation No. 20-71-10048 "Mathematical modeling of pathological behavior in multiplex networks arising as a result of dysfunction of single elements in application to biomedicine problems" researchers of Laboratory of topological methods in dynamics Kuptsov P.V., Stankevich N.V. a universal neural network map has been developed that reproduces the dynamics of various dynamical systems defined by ordinary differential equations. The map is built as an artificial neural network, the weights of which encode the simulated system. Different systems correspond to the same network structure with different values of weight coefficients adjusted during training. The training assumes that the equations of the system are known, and training datasets are prepared using these equations. The learning process takes into account, among other things, variations in the control parameters of the system, so that the resulting neural network model is able to reproduce scenarios of bifurcations of the system being modeled. Theoretical significance of the study - a new universal model of a dynamical system is proposed.

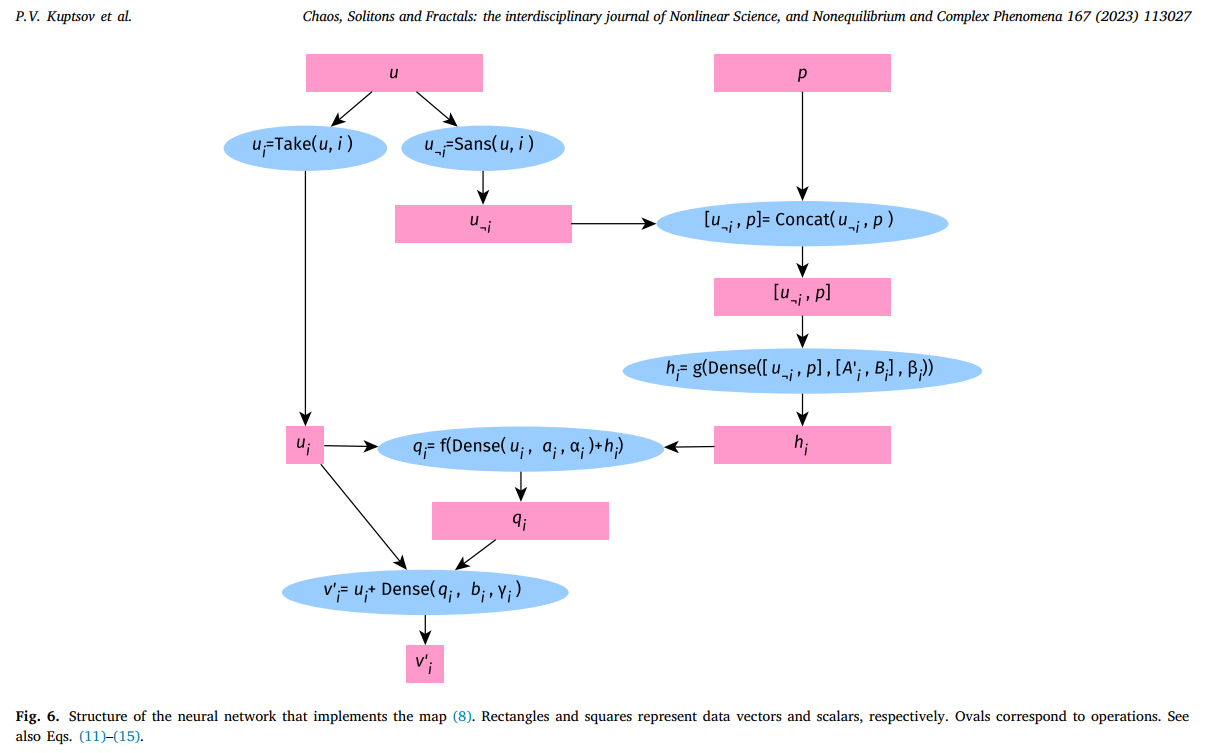
The minimal configuration network turned out to be unable to adequately model the behavior of a physiological neuron functioning in accordance with the Hodgkin-Huxley formalism. The reason is that such a system is essentially stiff, that is, it has two strong different time scales for changing dynamic variables. Therefore, a neural network model of a more complex configuration was developed, the main idea of which is the separation of learning for each dynamic variable. This approach made it possible to obtain a good correspondence between the dynamics of the neural network mapping and the original mathematical model [2]. In addition, an interesting effect was discovered: the neural network map was able to detect bistability in the original system, despite the fact that the training data explicitly represented the trajectories on only one of the two coexisting attractors. This effect can be used to search for so-called "rare attractors" - solutions of dynamical systems that coexist with the already known and have very small basins of attraction.

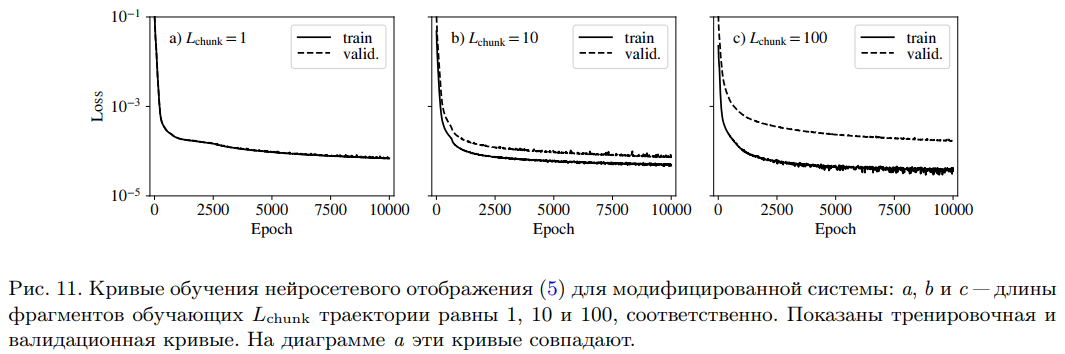
Neural network modeling has also been applied to systems of interacting physiological neurons. It was shown that a coupling can be introduced between neural network maps trained for single physiological neurons, and without additional training such a system will model the dynamics of a system of coupled neural oscillators. This means that due to the effect, which is called the ability of neural networks to generalize, single subsystems in the course of training do not just acquire the ability to generate trajectories of the simulated system. They also "reveal" its general properties, so that when a coupling is introduced, a neural network model of interacting physiological neurons is obtained, which reproduces the dynamics of the original system with high accuracy.

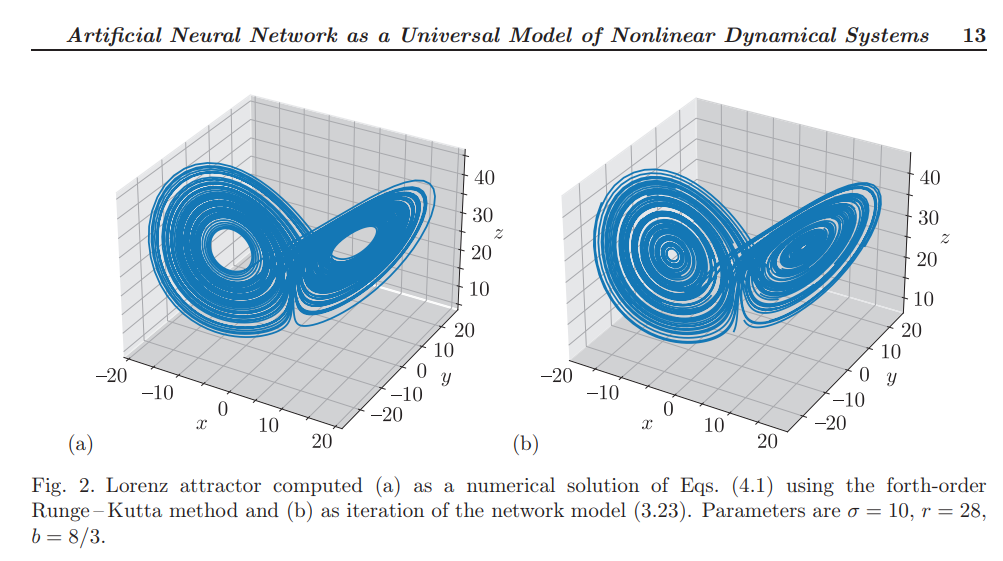
The proposed neural network map can be considered as a new universal design for modeling complex dynamics. Unlike models based on expansion into series (power, trigonometric), neural network map does not require the rejection of higher terms. Therefore, it allows modeling processes with an arbitrary order of nonlinearity, and for this reason there is reason to believe that in some aspects it will be more effective. In addition, it can be expected that, due to its ability to generalize, the network, even in the presence of a limited amount of data, will be able to extract from them information about dynamic phenomena that is not available to other modeling methods.

The approach developed in the work based on the use of neural network map can be considered in a sense as an alternative to traditional numerical methods for modeling dynamics. This approach is made relevant by the current rapid development of technologies for creating high-speed computing equipment that supports the training and operation of neural networks. We plan to develop this direction. It is interesting to further study the interaction of oscillators trained in isolation, when the coupling has a more complex form. For example, for networks of neurons, this could be a synaptic connection, which is mathematically described by a sigmoid function.

 

(с) Kuptsov Pavel

[1] Kuptsov P.V., Kuptsova A.V., Stankevich N.V. Artificial Neural Network as a Universal Model of Nonlinear Dynamical Systems Rus. J. Nonlin. Dyn. 2021. Т. 17, №1. С. 5-21.

[2] Kuptsov, P. V., Stankevich, N. V., Bagautdinova, E. R. Discovering dynamical features of Hodgkin-Huxley-type model of physiological neuron using artificial neural network. Chaos, Solitons & Fractals 2023, Т. 167, С. 113027.

[3] Купцов П.В., Станкевич Н.В. Моделирование динамики нейронных осцилляторов типа Ходжкина-Хаксли при помощи нейронной сети. «Известия высших учебных заведений. Прикладная нелинейная динамика» 2023. (submitted).

 

The results were discussed at the seminar of the Laboratory of Dynamical Systems and Applications on April 19, 2023.