Разработана нейронная сеть, моделирующая поведение широкого круга динамических система, в том числе системы типа Ходжкина-Хаксли, а также ансамблей на их основе

О ведущихся исследованиях

В рамках проекта РНФ № 20-71-10048 «Математическое моделирование патологического поведения в мультиплексных сетях, возникающего в результате дисфункции одиночных элементов, в приложении к задачам биомедицины» сотрудниками лаборатории топологических методов в динамике Купцовым П.В., Станкевич Н.В. разработано универсальное нейросетевое отображение, воспроизводящие динамику различных динамических систем, задаваемых обыкновенными дифференциальными уравнениями. Отображение построено как искусственная нейронная сеть, веса которой кодируют моделируемую систему. Разным системам отвечает одна и та же структура сети с разными значениями весовых коэффициентов, настраиваемых в ходе обучения. При обучении предполагается, что уравнения системы  известны, и обучающие наборы данных готовятся с использованием этих уравнений. В процессе обучения учитываются, в том числе и вариации управляющих параметров системы, так что получаемая нейросетевая модель умеет воспроизводить сценарии бифуркаций моделируемой системы. Теоретическая значимость исследования — предложена новая универсальная модель динамической системы.

 

В минимальной конфигурации нейросетевое отображение представляет собой нейронную сеть из двух полносвязных слоёв. Для её обучения используется стандартная процедура на основе метода обратного распространения ошибки и алгоритма оптимизации Adam, который представляет собой модифицированный алгоритм градиентного спуска с автоматической подстройкой шага. Этот подход, в силу своей простоты, позволяет даже на сравнительно маломощном вычислительном оборудовании за небольшое время обучать сети, которые с высокой точностью моделируют классические модели нелинейной динамики, такие как система Лоренца, система Ресслера, система Хиндмарша-Роуза [1].

Рисунок из статьи [1]

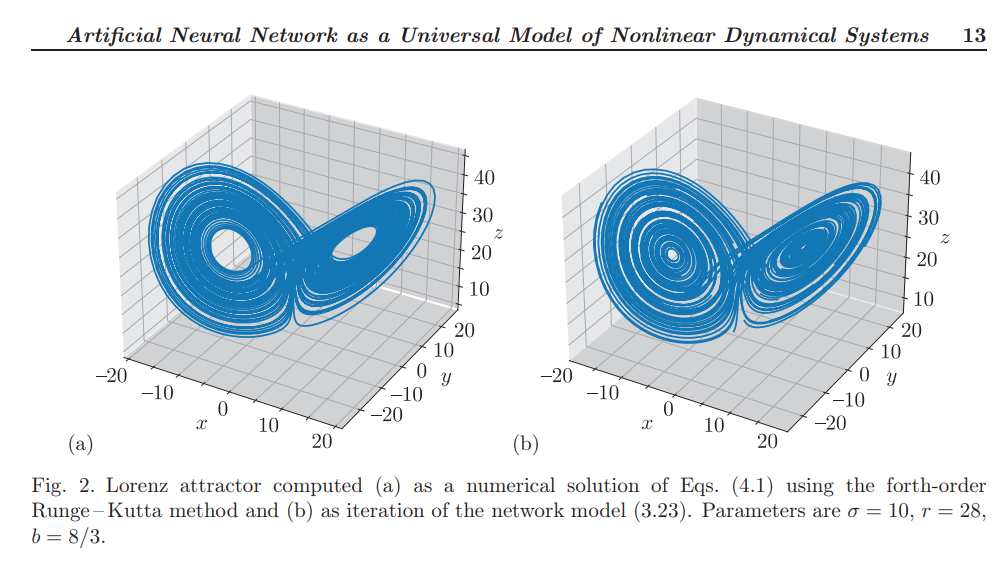
Сеть минимальной конфигурации оказалась не в состоянии на должном уровне моделировать поведение  физиологического нейрона, функционирующего в соответствии с формализмом Ходжкина-Хаксли. Причина в том, что такая система существенно жёсткая, то есть имеет два сильно отличающихся временных масштаба изменения динамических переменных. Поэтому была разработана нейросетевая модель более сложной конфигурации, основная идея которой — разделение обучения по каждой динамической переменной. Такой подход позволил получить хорошее соответствие динамики нейросетевого отображения и исходной математической модели [2]. Кроме того, был обнаружен интересный эффект — нейросетевое отображение сумело обнаружить бистабильность в исходной системе при том, что в обучающих данных были явно представлены траектории только на одном из двух сосуществующих аттракторов. Этот эффект может быть использован для поиска так называемых «редких аттракторов» — решений динамических систем, сосуществующих с уже известным и имеющими очень малые бассейны притяжения.

Рисунок из статьи 2

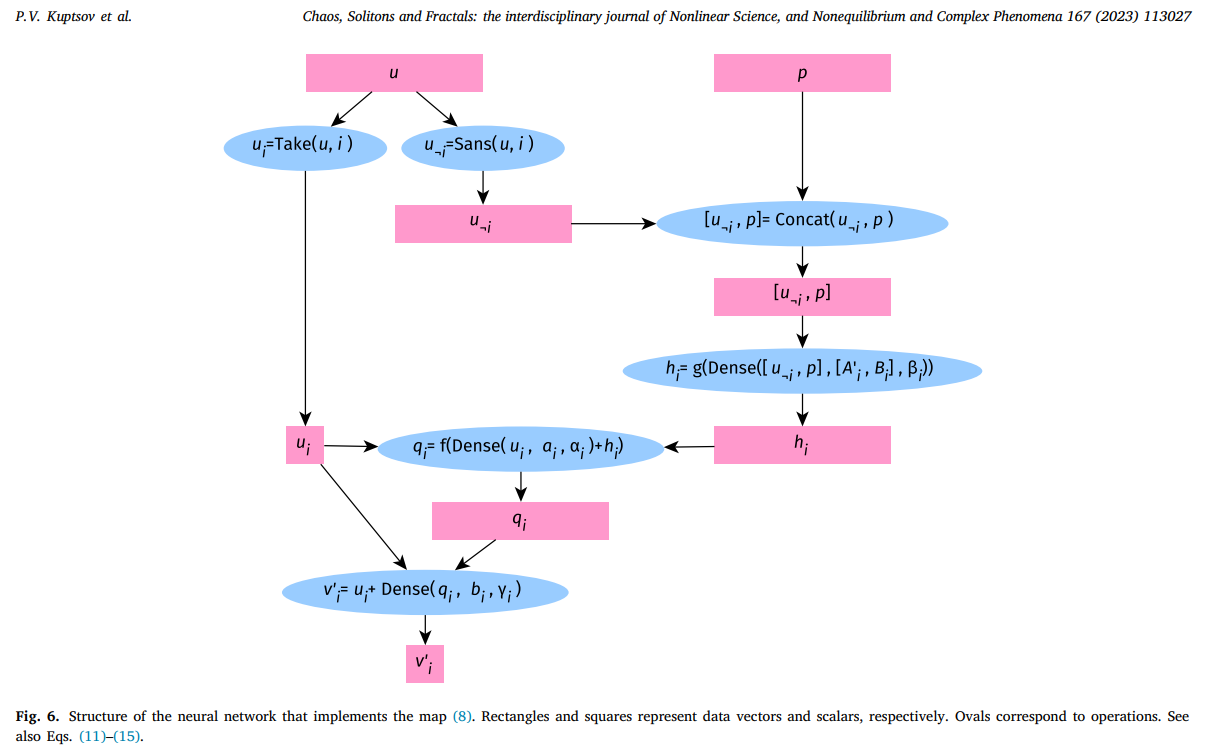
Нейросетевое моделирование было также применено к системам взаимодействующих физиологических нейронов. Было показано, что между нейросетевыми отображениями, обученными для одиночных физиологических нейронов, можно ввести связь, и без дополнительного обучения такая система будет моделировать динамику системы связанных нейронных осцилляторов. Это означает, что благодаря эффекту, который называют способностью нейронных сетей к обобщению, одиночные подсистемы в ходе обучения не просто приобретают возможность генерировать траектории моделируемой системы. Они также «выявляют» её общие свойства, так что при введении связи, получается нейросетевая модель взаимодействующих физиологических нейронов, которая с высокой точностью воспроизводит динамику исходной системы.

Рисунок из статьи [3]

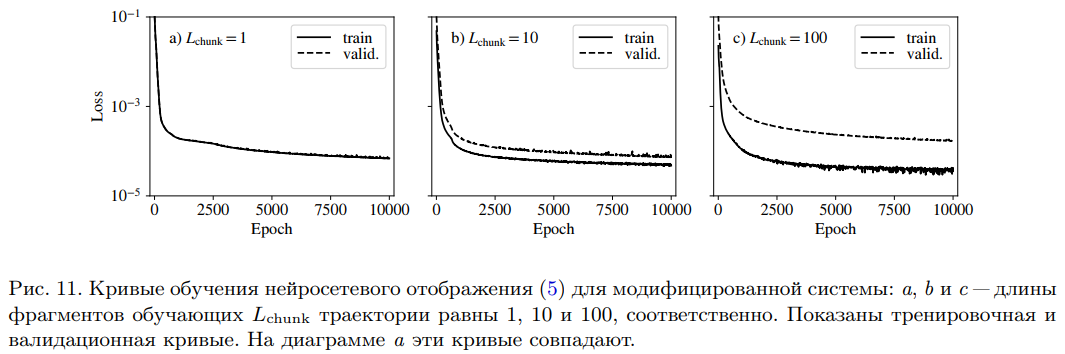
Предложенное нейросетевое отображение может рассматриваться как новая универсальная конструкция для моделирования сложной динамики. В отличие от моделей на основе разложения в ряды (степенные, тригонометрические), нейросетевое отображение не требует отбрасывания старших членов. Следовательно, оно позволяет моделировать процессы с произвольным порядком нелинейности, и по этой причине есть основания полагать, что в некоторых аспектах оно окажется более эффективным. Кроме того, можно ожидать, что, благодаря своей способности к обобщению, сеть, даже при наличии ограниченного количества данных, будет в состоянии извлекать из них информацию о динамических феноменах, недоступную для других методов моделирования.

«Развитый в работе подход на основе использования нейросетевого отображения можно рассматривать в некотором смысле как альтернативу традиционным численным методам моделирования динамики. Актуальным этот подход делает бурное развитие в настоящее время технологий создания быстродействующего вычислительного оборудования, поддерживающего обучение и работу нейронных сетей. Мы планируем развивать данное направление. Интересным представляется дальнейшее исследование взаимодействия обученных изолированно осцилляторов, когда связь имеет более сложное устройство. Например, для сетей нейронов, этом может быть синаптическая связь, которая математически описывается сигмоидной функцией»

(с) Купцов Павел Владимирович

По данным результатам подготовлено 3 статьи:

[1] Kuptsov P.V., Kuptsova A.V., Stankevich N.V. Artificial Neural Network as a Universal Model of Nonlinear Dynamical Systems Rus. J. Nonlin. Dyn. 2021. Т. 17, №1. С. 5-21.

[2] Kuptsov, P. V., Stankevich, N. V., Bagautdinova, E. R. Discovering dynamical features of Hodgkin-Huxley-type model of physiological neuron using artificial neural network. Chaos, Solitons & Fractals 2023, Т. 167, С. 113027.

[3] Купцов П.В., Станкевич Н.В. Моделирование динамики нейронных осцилляторов типа Ходжкина-Хаксли при помощи нейронной сети. «Известия высших учебных заведений. Прикладная нелинейная динамика». (направлена в журнал).

 

Получены два свидетельства о регистрации программы ЭВМ:

Купцов П.В., Купцова А.В., Станкевич Н.В. Нейронная сеть, моделирующая поведение динамических систем. Свидетельство о государственной регистрации программы ЭВМ №2021668593 от 18 ноября 2021.

Купцов П. В., Станкевич Н. В. Нейросетевая модель динамической системы с существенно разными временными масштабами изменения переменных. Свидетельство о государственной регистрации программы ЭВМ №2022665820 от 22 августа 2022: 

 

Результаты обсуждались на семинаре Междунаародной лаборатории динамических систем и приложений 19 апреля 2023г.